Abie Amadea Harahap

Rabu, 23 November 2011

TIK Jaringan Internet

Pengertian Jaringan Internet

Jaringan Internet jaman sekarang sudah berkembang pesat. Sesuai dengan selogan "Dunia ada di gengam tangan anda" merupakan selogan dari teknologi yang pesat yaitu internet. Jaringan Internet merupakan jaringan yang kompleks dan mengamgumkan di dunia maya sekarang itu merupakan pengertian jaringan internet. Manfaat Internet ada yang positif dan ada juga negatif. Bahkan anak SD sekarang sudah bisa mengakses Internet.

Internet adalah jaringan komputer yang bisa dikategorikan sebagai WAN, menghubungkan berjuta komputer diseluruh dunia, tanpa batas negara, dimana setiap orang yang memiliki komputer dapat bergabung ke dalam jaringan ini hanya dengan melakukan koneksi ke penyedia layanan internet (internet service provider / ISP) seperti Telkom Speedy, atau IndosatNet. Internet dapat diterjemahkan sebagai international networking (jaringan internasional), karena menghubungkan komputer secara internasional, atau sebagai internetworking (jaringan antar jaringan) karena menghubungkan berjuta jaringan diseluruh dunia.

Sejarah internet Indonesia dimulai pada awal tahun 1990-an. Saat itu jaringan internet di Indonesia lebih dikenal sebagai paguyuban network, dimana semangat kerjasama, kekeluargaan & gotong royong sangat hangat dan terasa di antara para pelakunya. Agak berbeda dengan suasana Internet Indonesia pada perkembangannya kemudian yang terasa lebih komersial dan individual di sebagian aktivitasnya, terutama yang melibatkan perdagangan Internet. Sejak 1988, ada pengguna awal Internet di Indonesia yang memanfaatkan CIX (Inggris) dan Compuserve (AS) untuk mengakses internet.

Matematika Trigonometri

Sejarah awal

Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu. Matematikawan India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri. Lagadha adalah matematikawan yang dikenal sampai sekarang yang menggunakan geometri dan trigonometri untuk penghitungan astronomi dalam bukunya Vedanga, Jyotisha, yang sebagian besar hasil kerjanya hancur oleh penjajah India.
Matematikawan Yunani Hipparchus sekitar 150 SM menyusun tabel trigonometri untuk menyelesaikan segi tiga.
Matematikawan Yunani lainnya, Ptolemy sekitar tahun 100 mengembangkan penghitungan trigonometri lebih lanjut.
Matematikawan Silesia Bartholemaeus Pitiskus menerbitkan sebuah karya yang berpengaruh tentang trigonometri pada 1595 dan memperkenalkan kata ini ke dalam bahasa Inggris dan Perancis.

Trigonometri sekarang ini

Ada banyak aplikasi trigonometri. Terutama adalah teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat, dalam geografi untuk menghitung antara titik tertentu, dan dalam sistem navigasi satelit.
Bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging (CAT scan dan ultrasound), farmasi, kimia, teori angka (dan termasuk kriptologi), seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanik, teknik sipil, grafik komputer, kartografi, kristalografi.
Ada pengembangan modern trigonometri yang melibatkan "penyebaran" dan "quadrance", bukan sudut dan panjang. Pendekatan baru ini disebut trigonometri rasional dan merupakan hasil kerja dari Dr. Norman Wildberger dari Universitas New South Wales. Informasi lebih lanjut bisa dilihat di situs webnya

Hubungan fungsi trigonometri

$\tan A = \frac{\sin A}{\cos A}\,$

$\cot A = \frac{1}{\tan A} = \frac{\cos A}{\sin A}\,$

$\sec A = \frac{1}{\cos A}\,$

$\csc A = \frac{1}{\sin A}\,$

Identitas trigonometri

$\sin^2 A + \cos^2 A = 1 \,$

$1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,$

$1 + \cot^2 A = \frac{1}{\sin^2 A} = \csc^2 A \,$

Penjumlahan

$\sin (A + B) = \sin A \cos B + \cos A \sin B \,$

$\sin (A - B) = \sin A \cos B - \cos A \sin B \,$

$\cos (A + B) = \cos A \cos B - \sin A \sin B \,$

$\cos (A - B) = \cos A \cos B + \sin A \sin B \,$

$\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \,$

$\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \,$

Rumus sudut rangkap dua

$\sin 2A = 2 \sin A \cos A \,$

$\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,$

$\tan 2A = {2 \tan A \over 1 - \tan^2 A} = {2 \cot A \over \cot^2 A - 1} = {2 \over \cot A - \tan A} \,$

Rumus sudut rangkap tiga

$\sin 3A = 3 \sin A - 4 \sin^3 A \,$

$\cos 3A = 4 \cos^3 A - 3 \cos A \,$

Rumus setengah sudut

$\sin \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{2}} \,$

$\cos \frac{A}{2} = \pm \sqrt{\frac{1+\cos A}{2}} \,$

$\tan \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} \,$

Bahasa Indonesia Puisi

Puisi (dari bahasa Yunani kuno: ποιέω/ποιῶ (poiéo/poió) = I create) adalah seni tertulis di mana bahasa digunakan untuk kualitas estetiknya untuk tambahan, atau selain arti semantiknya.
Penekanan pada segi estetik suatu bahasa dan penggunaan sengaja pengulangan, meter dan rima adalah yang membedakan puisi dari prosa. Namun perbedaan ini masih diperdebatkan. Beberapa ahli modern memiliki pendekatan dengan mendefinisikan puisi tidak sebagai jenis literatur tapi sebagai perwujudan imajinasi manusia, yang menjadi sumber segala kreativitas. Selain itu puisi juga merupakan curahan isi hati seseorang yang membawaa oraang lain kedaalam keaadaan hatinya.
Baris-baris pada puisi dapat berbentuk apa saja (melingkar, zigzag dan lain-lain). Hal tersebut merupakan salah satu cara penulis untuk menunjukkan pemikirannnya. Puisi kadang-kadang juga hanya berisi satu kata/suku kata yang terus diulang-ulang. Bagi pembaca hal tersebut mungkin membuat puisi tersebut menjadi tidak dimengerti. Tapi penulis selalu memiliki alasan untuk segala 'keanehan' yang diciptakannya. Tak ada yang membatasi keinginan penulis dalam menciptakan sebuah puisi. Ada beberapa perbedaan antara puisi lama dan puisi baru
Namun beberapa kasus mengenai puisi modern atau puisi cyber belakangan ini makin memprihatinkan jika ditilik dari pokok dan kaidah puisi itu sendiri yaitu 'pemadatan kata'. kebanyakan penyair aktif sekarang baik pemula ataupun bukan lebih mementingkan gaya bahasa dan bukan pada pokok puisi tersebut.
Didalam puisi juga biasa disisipkan majas yang membuat puisi itu semakin indah. Majas tersebut juga ada bemacam, salah satunya adalah sarkasme yaitu sindiran langsung dengan kasar.
Dibeberapa daerah di Indonesia puisi juga sering dinyanyikan dalam bentuk pantun. Mereka enggan atau tak mau untuk melihat kaidah awal puisi tersebut.

Fisika Momentum

Dalam mekanika klasik, momentum (dilambangkan dengan P) didefinisikan sebagai hasil perkalian dari massa dan kecepatan, sehingga menghasilkan vektor.
Momentum suatu benda (P) yang bermassa m dan bergerak dengan kecepatan v didefinisikan sebagai ::

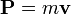
$\mathbf{P}= m \mathbf{v}\,\!$

Massa merupakan besaran skalar, sedangkan kecepatan merupakan besaran vektor. Perkalian antara besaran skalar dengan besaran vektor akan menghasilkan besaran vektor. Jadi, momentum merupakan besaran vektor. Momentum sebuah partikel dapat dipandang sebagai ukuran kesulitan untuk mendiamkan benda. Sebagai contoh, sebuah truk berat mempunyai momentum yang lebih besar dibandingkan mobil yang ringan yang bergerak dengan kelajuan yang sama. Gaya yang lebih besar dibutuhkan untuk menghentikan truk tersebut dibandingkan dengan mobil yang ringan dalam waktu tertentu. (Besaran mv kadang-kadang dinyatakan sebagai momentum linier partikel untuk membedakannya dari momentum angular).

Hukum Kekekalan Momentum

Sama seperti energi, dalam kondisi tertentu, momentum suatu sistem akan kekal atau tidak berubah. Untuk memberikan pemahaman mengenai hal tersebut, maka akan digunakan konsep Pusat Massa. Misal jika ada sebuah sistem yang terdiri dari beberapa benda dengan massa $\mathbf{m_1}, \mathbf{m_2}, \mathbf{.....}.$ bergerak dengan kecepatan masing-masing adalah $\mathbf{v_1}, \mathbf{v_2}, \mathbf{.....}.$ , maka kecepatan pusat massa sistem tersebut adalah :

$\mathbf{v_{cm}} = { \displaystyle\sum m_i \mathbf{v}_i \over \displaystyle\sum m_i }.$

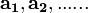Dan jika sistem tersebut bergerak dengan dipercepat dengan percepatan masing-masing adalah $\mathbf{a_1}, \mathbf{a_2}, \mathbf{.....}.$ , maka percepatan pusat massa sistem tersebut adalah :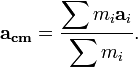

$\mathbf{a_{cm}} = { \displaystyle\sum m_i \mathbf{a}_i \over \displaystyle\sum m_i }.$

Sekarang jika benda-benda tersebut masing-masing diberi gaya $\mathbf{F_1}, \mathbf{F_2}, \mathbf{.....}.$ , maka benda-benda tersebut masing-masing memiliki percepatan :

$\mathbf{a_{i}} = { \mathbf{F_i} \over m_i }.$

Sehingga percepatan pusat massa sistem dapat dinyatakan sebagai :

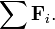$\mathbf{a_{cm}} = { \displaystyle\sum \mathbf{F}_i \over \displaystyle\sum m_i }.$

Notasi $\displaystyle\sum \mathbf{F}_i.$ merupakan notasi yang menyatakan resultan gaya yang bekerja pada sistem tersebut. Jika resultan gaya yang bekerja pada sistem bernilai nol ( $\displaystyle\sum \mathbf{F}_i = 0$ ), maka sistem tersebut tidak dipercepat ( $\displaystyle\sum \mathbf{a}_i = 0$ ). Jika sistem tidak dipercepat, artinya sistem tersebut kecepatan pusat massa sistem tersebut konstan ( $\mathbf{v_{cm}} = constant$ ). Jadi dapat disimpulkan bahwa :

$\displaystyle\sum m_i \mathbf{v}_i = constant.$

Notasi di atas merupakan notasi dari hukum kekekalan momentum. Jadi total momentum suatu sistem akan selalu kekal hanya jika resultan gaya yang bekerja pada sistem tersebut bernilai nol.

Minggu, 13 November 2011

Matematika Aljabar

Penemu Aljabar adalah Abu Abdullah Muhammad Ibn Musa al-Khwarizmi. Aljabar berasal dari Bahasa Arab "al-jabr" yang berarti "pertemuan", "hubungan" atau "perampungan" adalah cabang matematika yang dapat dicirikan sebagai generalisasi dari bidang aritmatika. Aljabar juga merupakan nama sebuah struktur aljabar abstrak, yaitu aljabar dalam sebuah bidang.

Jenis-jenis Aljabar

Aljabar dapat dipilah menjadi kategori berikut:

Aljabar dasar, yang mencatat sifat-sifat operasi bilangan riil, menggunakan simbol sebagai "pengganti" untuk menandakan konstanta dan variabel, dan mempelajari aturan tentang ungkapan dan persamaan matematis yang melibatkan simbol-simbol tersebut.

Aljabar abstrak, yang secara aksiomatis mendefinisikan dan menyelidiki struktur aljabar seperti kelompok matematika, cincin matematika dan matematika bidang.

Aljabar linear, yang mempelajari sifat-sifat khusus ruang vektor (termasuk matriks).

Aljabar universal, yang mempelajari sifat-sifat yang dimiliki semua struktur aljabar.

Aljabar komputer, yang mengumpulkan manipulasi simbolis benda-benda matematis.

Pengertian bentuk aljabar

Bentuk-Bentuk seperti 2a , -5b, x3, 3p + 2q disebut bentuk aljabar.Pada bentuk aljabar 2a, 2 disebut koefisien, sedangkan a disebut variabel( peubah ).

Persamaan dan pertidaksamaan linear

Persamaan Linear Satu Variabel

Persamaan Linear Satu Variabel berarti persamaan pangkat satu. Pada persamaan linear ini berlaku hukum :

Ruas kiri dan ruas kanan dapat ditambahkan atau dikurangi bilangan yang sama
Ruas kiri dan ruas kanan dapat dikalikan atau dibagi dengan bilangan yang sama.

Contoh :

r:10

1. r + 3 = 10.

r + 3 - 3 = 10 - 3 (sama sama dikurangi dengan bilangan yang sama yaitu 3)
  r = 7

2. 3p = 12

3p / 3 = 12/3 (sama-sama dibagi dengan bilangan yang sama yaitu 3)
  p = 4

Pertidaksamaan Linear satu variabel

Pertidaksamaan linear satu variabel berarti kalimat terbuka yang memiliki tanda <,>, Pada persamaan linear berlaku hukum:

Ruas Kiri dan kanan dapat ditambah, dikurangi, dikali, atau dibagi bilangan yang sama
jika variabel bertanda minus, harus diganti menjadi positif dengan mengali bilangan negatif dan membalikan tanda

contoh : 1. 5v - 7 > 23

5v - 7 + 7 > 23 + 7
  5v / 5 > 30 / 5
  v > 6

2. -2a < 10

-2a / -2 > 10 / -2
  a > -5\

3. -2a < 10

-2a / -2 > 10 / -2
  a > -5\

Kamis, 03 November 2011

First Post

Ini adalah post pertama pada blog ini.